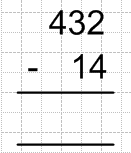
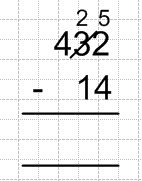The numerical difference between 1 and 2 is the same as that between 0 and 1, but they are not the same. I cite some examples:
1. When sharing food, and there's only one piece left, nobody touches the food. Every time you take away a piece, you deprive others of having another piece. This deprivation is greatest when you take away the last piece, compared to any other pieces. Suddenly from having food in the plate, there's none left now. The more pieces there are, the less the deprivation from taking away one piece. Hence, the speed of taking food from a plate full of it is very fast initially but decays rapidly to near zero when it approaches the last piece. Especially between strangers.
2. Going from 0 pull up to 1 pull up is tremendously difficult. Going from 1 to 2 is easier than going from 0 to 1. I think 90% of the effort is spent training to go from 0 to 1 than any other increment. So the real question is this: Can you do one? If you can, you can do a lot more!
3. If the price of an item decreases from $2 to $1, it's quite different from dropping from $1 to $0, even thought the drop is still $1. What's $0? It's free! Free is so powerful that it makes people want something even though they don't need it. Conversely, an item that is free initially, once you start charging money for it, you'll howls of protest. If you've offered free water and start charging for it now, you better have some PR skills out there.
This has some implication in doing certain things differently.
When you're selling things to others, you might want them to buy something small from you first. This could be the opener to other things. Once they get over the hurdle of buying anything from you, effectively crossing the great gulf from 0 to 1, you can convince them to buy more things from you. This is a trick that is used in bargain shops. One or two items might be very cheap compared to the rest of the market, but when you're there and you bought it, you've just crossed the distance between 0 and 1. It makes it more likely for you to buy any other things since you're already there. Change a non-interested person to an interested person, from an interested person to a small buyer, from a small buyer to a large buyer.
When negotiating, make the other party concede to something small first, effectively breaking their resistance to bigger concessions. Once they crossed the gulf from 0 to 1, it'll be easier to ask them to concede more.
When building confidence, start by doing small things that makes you feel confident. You might want to start a weight loss program and didn't have the motivation to start. Buy yourself a new shoe, go down and just walk first. Once you get over that big jump from 0 to 1, progressively increase it, making sure you build the confidence to clear small hurdles before climbing bigger ones.
Mathematics is funny when applied to real life with all our emotions invested in our actions. 2 minus 1 is really different from one minus zero.
1. When sharing food, and there's only one piece left, nobody touches the food. Every time you take away a piece, you deprive others of having another piece. This deprivation is greatest when you take away the last piece, compared to any other pieces. Suddenly from having food in the plate, there's none left now. The more pieces there are, the less the deprivation from taking away one piece. Hence, the speed of taking food from a plate full of it is very fast initially but decays rapidly to near zero when it approaches the last piece. Especially between strangers.
2. Going from 0 pull up to 1 pull up is tremendously difficult. Going from 1 to 2 is easier than going from 0 to 1. I think 90% of the effort is spent training to go from 0 to 1 than any other increment. So the real question is this: Can you do one? If you can, you can do a lot more!
3. If the price of an item decreases from $2 to $1, it's quite different from dropping from $1 to $0, even thought the drop is still $1. What's $0? It's free! Free is so powerful that it makes people want something even though they don't need it. Conversely, an item that is free initially, once you start charging money for it, you'll howls of protest. If you've offered free water and start charging for it now, you better have some PR skills out there.
This has some implication in doing certain things differently.
When you're selling things to others, you might want them to buy something small from you first. This could be the opener to other things. Once they get over the hurdle of buying anything from you, effectively crossing the great gulf from 0 to 1, you can convince them to buy more things from you. This is a trick that is used in bargain shops. One or two items might be very cheap compared to the rest of the market, but when you're there and you bought it, you've just crossed the distance between 0 and 1. It makes it more likely for you to buy any other things since you're already there. Change a non-interested person to an interested person, from an interested person to a small buyer, from a small buyer to a large buyer.
When negotiating, make the other party concede to something small first, effectively breaking their resistance to bigger concessions. Once they crossed the gulf from 0 to 1, it'll be easier to ask them to concede more.
When building confidence, start by doing small things that makes you feel confident. You might want to start a weight loss program and didn't have the motivation to start. Buy yourself a new shoe, go down and just walk first. Once you get over that big jump from 0 to 1, progressively increase it, making sure you build the confidence to clear small hurdles before climbing bigger ones.
Mathematics is funny when applied to real life with all our emotions invested in our actions. 2 minus 1 is really different from one minus zero.